The quality of the mesh guarantees the best analysis results for the problem, minimizing the need for additional analysis runs and improving one's predictive capabilities.

Structured Block Meshes

The key to building a quality mesh is to use structured blocks. TrueGrid^®'s standard parts are based on hexahedral solid elements and quadrilateral thin shell elements. They are arranged in rows, columns, and layers to form structured blocks. Structured blocks are preferred because it is possible to control the quality of the mesh and to decompose the problem into manageable pieces.

In order to demonstrate the importance of multiple block technology to the construction of quality meshes, consider the problem of meshing the inside of a circle with quadrilateral elements.

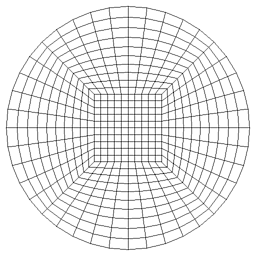
	Take a single block and form a circle. This produces 4 elements, corresponding to the four corners of the block, that are extremely distorted. Each corner is almost 180 degrees. The more elements used to model the circle, the closer the angles get to 180 degrees. In many simulations, the magnitude of the physical quantities are largest along the exterior. The mesh is at its worst where a quality mesh is needed most.
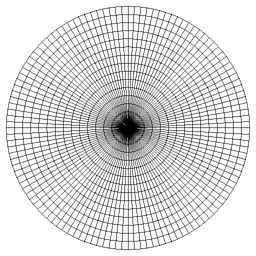
	Another approach places the mesh irregularities at the center. This has some drawbacks, as well, by placing poorly shaped triangular elements together at the center of the mesh. The more refined the mesh becomes, the worse the triangles get. This increases the bandwidth for implicit solvers.
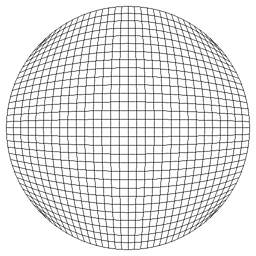
	Now place the irregularities between the boundary and the center by using a 5 block part. There are 4 irregularities in the mesh, located where only three elements meet at an interior node. These irregularities are not as severe, since the average angle at these nodes is 120, only 33% away from the ideal of 90 degrees. No matter how many elements are used in this structure, the irregularities do not get worse.

This multiple block part technique to form curved objects is commonly used. The 3D analogue of the circle is the sphere. In this example, there is a single cube at the center of the sphere, with 6 more blocks, each extruding from one of the 6 faces of the center cube. TrueGrid® is designed to make multiple block parts easy to build.

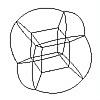
Algebraic Interpolation

With structured blocks, mesh generation can then be reduced to the fundamental notion of a multi-variable vector function. All of classical mathematics and many modern techniques can then be applied to the mesh generation problem. For example, the best algebraic mesh generation methods such as transfinite interpolation are based on 3 dimensional vector functions with rectangular domains in the 3D computational space and with ranges in the 3D physical space.

Smoothing With Elliptic Solvers

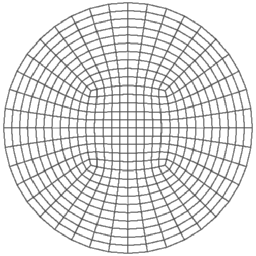
Smooth meshes are the solutions to a system of elliptic partial differential equations. TrueGrid® supports the equipotential relaxation, uniform smoothing, and the Thomas-Middlecoff elliptic methods. The first method tries to equalize the zoning as it gets away from the boundary. The second method is an improvement when boundaries have large curvatures. The last method carries the nodal distribution throughout the interior. All produce near orthogonal meshes.

Nodal Density and Numerical Error

The finite difference method for solving partial differential equations is a powerful technique in numerical simulations. The accuracy of this method can be estimated by using a truncated Taylor series expansion of the solution at neighboring grid points. These are substituted into the difference expressions to the partial differential equations. The resulting estimate of error is a function of the distance between the grid points and the magnitude of the gradient of the field variables being approximated in the numerical simulation.

To keep the numerical error at an acceptable and uniform level, it is best to decrease the distance between grid points where the gradients are high. Essentially, the mesh density must anticipate the gradient of the solution. This is why it is valuable to have some intuition about the solution when building the mesh. When intuition is not sufficient, then test runs are called for, where a coarse and possible simplified version of the mesh can be quickly and inexpensively run to gain insights into the problem. If the mesh generation is parametric, then one can gradually step-up the mesh to the full problem. In simple problems, the mesh can be uniformly dense. In most problems, however, there are never enough grid points to be wasted in areas where the gradients are small.

It is not sufficient to simply dump a lot of nodes in one area of the mesh. If the rate of change in the mesh density is large, then the accuracy of the solution in that area may go down. The transition from a coarse to a fine mesh must be done gradually to avoid introducing error due to abrupt changes in the mesh. There are no absolutes in this, but usually a 10% increase between neighboring cells or elements is tolerated, even in the presence of shocks.

Although finite element, finite volume, and other methods of solving partial differential equations cannot be analyzed in the same fashion, it turns out that they are equally sensitive to these same nodal density issues.

With TrueGrid^®, you control the distribution of nodes along edges of a block. Nodes can be equally spaced along the intersection of two surfaces forming an edge of the block. Nodes can be clustered near one end of an edge, both ends, or the middle. A nodal density distribution function can be defined to cluster nodes along an edge in an arbitrary fashion.

Nodal distribution can be controlled independently in all three directions. Several adjacent edges from several adjacent blocks can be treated as though they formed a composite edge for nodal distribution. The nodal distribution of a face of a block is inherited from the nodal distribution of its four bounding edges. The nodal distribution on the face will also depend on the type of interpolation and/or elliptic solver applied to the face as well as the curvature of the surface on which the face is projected. The nodal distribution of the interior of a block depends on the nodal distribution of its six bounding faces. Again, this nodal distribution will also depend on the type of interpolation and/or elliptic solver applied to the interior.

  Home Page

Questions, comments, suggestions

Copyright © 1996-2013 XYZ Scientific Applications, Inc. All rights reserved.